四色問題

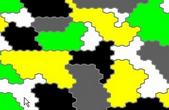
　三色パンのどこから口にすればいいのか、五目飯のどの具から箸をつければいいのか、頭を悩ませる人もいるだろう。だが、それはすぐに解決する。
　同じように数字がつく問題とはいえ、四色問題は違う。数学者は１５０年間も頭を悩ませてきたのだ。
　地図にある国に隣同士が同じ色にならないように色を付けていくとすると、最低何色あれば事足りるか、というのが四色問題だ。たとえば地図に１００の国があるとすると、１００色の色があれば、みんな違う色に塗り分けられるから、当然隣り合う国は違う色になる。直感でも９９，９８色あたりでも、できるような気がする。じゃあこの数字をいくつまで下げることができるだろう。このことを１５０年もの間、数学者は考えていたのだ。
　数学者には意外にケチが多いのだろうか。少々クレヨンが多くなってもいいじゃないか。これじゃ、最低生活を送るために必要な月々の小遣い問題と一緒だ。もう少し小遣い上げてもいいだろう。そう強く主張したい。

　まぁそれはさておき、実は経験的に四色あればできるってことがなんとなく分かってたんだけど、数学的に証明できてなかったのね。
で、１９８７年にコンピューターを使ってそれが証明されたことになったんだけど、そのプログラムがとても複雑で、そのプログラム自体の確かさが分からなかった。それが今回米国の研究者たちが、そうしたプログラムの正当性をチェックするソフトを開発した、というのがネタ元の記事だ。
　これで四色問題は本格的に解決ということになったらしい。
　でも本当にそうなのだろうか。では数学者にお尋ねしたい。
　日本海に浮かぶ孤島は一体何色なのか。ヨン様一色に染まった国のものなのか、それともヨン様の国のものなのか。
　どうだろう？答えるのはきっと難しいことだろう。
　これを新たなヨン色問題として提起したい。

ネタ元
Computer generates verifiable mathematics proof　19 April 2005