息子の数学の問題を考えていたとき、とても面白いことに気づいた。
2辺の長さが与えられれば三角形が決まるというものだ。
たとえばこんな風なabcの三角形があるとする。もちろんxはいろいろな長さがあるはずなのだが、あるアプローチをすると一意に決まるのだ。
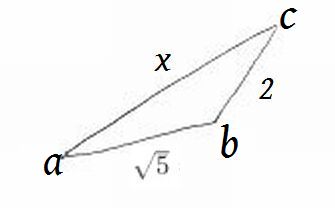
さっそくやってみよう。
この図のように直角になるような点Aを作図する。
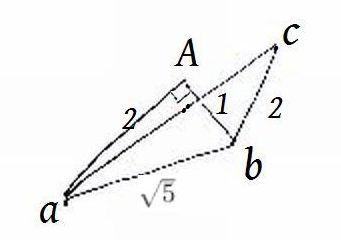
そしてそのAを上に持ち上げると三角錐ができる。
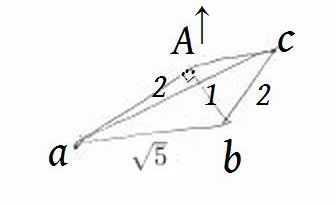
Aとcの長さはいろいろありなんでもいのだが、たとえば2としてみよう。
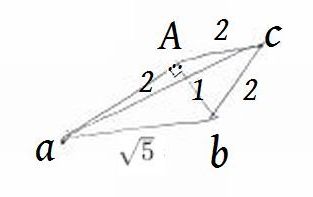
Aが直角なのでこの三角錐の体積の捉え方が二つで表現できる。
ひとつは 底面Abcとして高さAaつまり2の三角錐。
もうひとつは底面Aacとした高さAbつまり1の三角錐。
底面Abcの面積は三辺の長さが分かっているのでヘロンの公式などで確定できる。
であれば底面Aacのなかのacつまりxは求まるというわけだ。
二辺だけで三角形が確定されるなんて、いくらなんでもおかしい。普段この手の問題はビールをあおりながら考えるのだが、事態の深刻さにしらふでも考え続け、結局間違いに気づくのにずいぶん時間がかかってしまった。
とういうことで、ビールを引っかけなくても、引っかかった問題をメモしておく。