ゲームの回答者の前に三つのドア(#1,#2,#3)があって、そのうち一つのドアの後ろだけに豪華賞品がおかれている。ここで回答者が正しくない答え、たとえばドア#1を選んだとする。すると司会のモンティが、商品がドア#2の後ろにはないことを明かし、回答者にそのままドア#1を選ぶか、それともドア#3に変えるかを聞く。さて回答者はどうするべきか?
これは実際に米国のTVで行われていたモンティ・ホールが司会を務める視聴者参加番組の内容だ。高視聴率を稼いでいたが、番組打ち切り近くになってあるコラムニストから回答者が取るべき正しい対応についてのコメントがある雑誌に寄せられた。
回答者にとって有利な選択は、最初選択したものを放棄し、司会者が残したものを選ぶべきだというのだ。
このコメントに対しいろんな意見が寄せられ、素人から数学者まで加わるという侃々諤々の議論がわき起こり、ついにはコラムニストに対し廃業しろ的な批判も出たという。これがモンティ・ホール問題と呼ばれるものだと、本には述べられている。
コラムニストもきっと驚いたに違いない。騒動に対しだれが悪いというわけでもないのだろうが、それにしてもかなりめんどうな話のようだ。
もう一度、ゲームの進行を自分なりの言葉で表現してみる。
クイズの答え云々は考えなくてもいいだろう。ドアを三つの箱としよう。そのうちの一つだけに景品が隠されているというわけだ。回答者はどれかを勘で選ぶ。
その状態でどの箱に景品があるかを知っている司会者が、回答者が選んだものでない残り二つのうち、景品の入っていない箱を取り除く。
そして回答者はこう聞かれるのだ。「そのままでいいですか、それとも変えますか?」
どちらか一方に景品が入っていることは間違いなく、これも山勘で選ぶしかない。
どちらを選んでも景品が入っている確率は五分五分じゃないの?
誰しもそう考えるのではないだろうか。だが、それが違うというのだ。回答者は最初自分が選んだものとは違う、司会者が残した方を選ぶと二倍の確率で景品にありつけるという。これがコラムニストが寄せた内容だった。
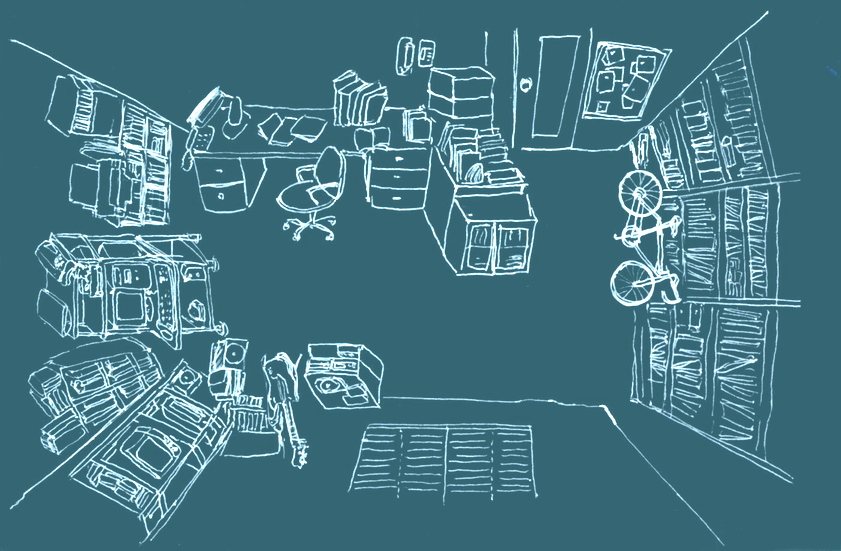
いろいろな視点からの説明がしてあるが、どうもしっくりこない。写真の絵もその一つだ。これだけでは分かりにくいかもしれないが、文字で説明するのも大変なのでなにか参考になればと拝借してみた。
実はこの絵は同じ問題が紹介されていた以前読んだ本からのもので、そのときもよく分からないままであった。そのいくつかの説明の一つに実際にやってみれば分かる、というのがあったので、少しは進歩してみようかとスクリプトを書いてみた。クリック
その過程で理解できたのは、つまりは回答者がランダムに選んだ箱とランダムに景品が入っている箱との一致が、最初選んだときのままと選択を変えたときではどう変わるかという問題に帰結するのではないかということだ。
ということで、スクリプトでやったことはランダムに回答者に箱を選ばせ、ランダムに景品を箱に入れ、もう一度回答者にランダムに箱を変更させるということだ。
ランダムに選んだ箱とランダムに変更した箱が一致すれば変更しなかったということで、違えば変更したということになる。
この変更しなかったときと変更したときそれぞれについて、ランダムに入れた景品の箱が一致しているかどうかを見た。(ついでに景品をロスした回数も出している)
つまりは変更しなかったときと、変更したときの景品をゲットする回数を比較しているということになるはずだ。
するとどうだろう。数値をいろいろ変えてやってみても、やはり2倍近くになっているではないか。
もちろん思考の組み立てが間違っていたり、スクリプトがおかしかったりする可能性は大いにあるのだが、もしそうではないとすると、不思議なことにこの思考過程には司会者が取り除いた箱は出てこないのだ。
箱はどこにいったのか。そもそも箱を取り除く必要があったのか。
なんとも気モンティが悪い問題である。
今読んでいる本:「本能はどこまで本能か」
参考図:「数字に弱いあなたの驚くほど危険な生活」